大学受験の始め方：難関大学に入る勉強法

数学問題の解き方。

 

ポリアの「いかにして問題をとくか」を読む。

 

まず、求められている答えが何か、ハッキリさせます。

 

数学以外のセンター試験などではよく、「正しいものを選べ」とか「誤っているものを選べ」「適切でないものを選べ」などという、紛らわしい設問があります。

 

こういう場合、正しいものを選ぶのか誤っているものを選ぶのか、まずその部分に○をつけて、何を答えるのかをハッキリ印を付けておく必要があります。

 

そうしなければ、間違った選択肢を選んでしまいます。

数学でも紛らわしい表現があります。

 

• 「この図形の面積を求めよ」
• 「この図形の周の長さを求めよ」
• 「回転体の体積を求めよ」
• 「表面積を求めよ」

とでは、求めるものがまるで違いますから、同様の工夫が必要でしょう。

 

そして、与えられているデータや条件にも、しっかり印を付けておきましょう。

 

例題を用いれば、こんな感じです。

 

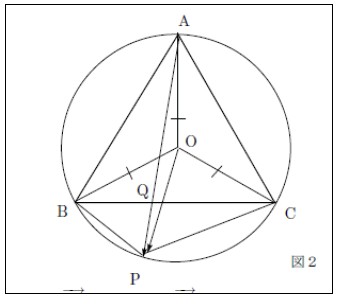
例題1 (30 点)円に内接する四角形ABP C は次の条件（ イ） ， （ロ）を満たすとする．（イ） 三角形ABC は正三角形である（ロ） AP とBC の交点は線分BC をp : 1 - p (0 < p < 1) の比に内分する．このときベクトルAP をベクトルAB，ベクトルAC， p を用いて表せ．

こういう風に、大事なところにマークをするという行為は、脳に重要なシグナルを与えます。

 

つまりマークをした時点で、脳は無意識にそれに関する知識を探し始めるのです。

 

問題を解いている最中に、足りない条件を探すような場合にも、マーキングは非常に役に立ちます。

 

条件が足りないな…と思って問題文を読み返すとき、マークがしてあるとすぐに見つけられるでしょう？
私の教えている生徒でも、マーキングを確実にやる生徒はどんどん上達しますが、バカにしてやらない生徒はなかなか成績が上がりません。

 

そんなもんです。

 

マーキングは、必ずやりましょう

 

問題を理解する（２ ）条件は、未知なものを定めるのに十分であるか？

 

与えられている条件だけで、答えを導き出せるものかどうか、それを考えます。

 

たとえばルートで表された文字式があった場合、ルートの中は負でないという、暗黙の条件が隠されていたりします。

 

そういう隠された条件が必要があるかどうかも、判断しなければなりません。

 

問題に書かれていない条件についても、考えましょう。

 

問題を理解する（３ ）図を描け、適当な記号を導入せよ

先ほどの例題の問題を図にすれば、右のような図になりますね。

 

中心Ｏ を描き入れたり、半径を書き入れて同じ大きさだと示す記号を入れたりすると、多少は見通しがつくはずです。

 

図形問題でなくても、数学は図や表を描くと視覚的に捉えやすくなります。

 

東京出版の「数学ショートプログラム」などによく載っていますが、数式でもなのにベクトルを考えると解きやすいとか、グラフにすれば分かるとか。

 

二次関数や三次関数などは、グラフを描くのは必須ですし、場合の数や確率なども、必ず書くようにしましょう。

 

図や表は、簡単な問題でも必ず書きましょう。

 

 

問題を理解する（４ ）条件の各部を分離せよ。

それを書き表すことができるか？

 

与えられた条件だけで問題が解けるとしても、そのまま使えるかどうかはわかりません。

 

ルートの中が負でない条件などを求め、別の条件から候補を絞り込み、の未知数を求める必要があります。

 

これを「条件の分離と、言い換え」といいますが、そういう作業が必要な問題も、よくあります。