大学受験の始め方：難関大学に入る勉強法

数学や物理には、山ほど公式があります。

 

が、皆さんは、まさか全部まる覚えしようとしていませんよね？

 

確かに覚えておいた方が便利な公式というのは、たくさんあります。

 

それに、覚えていればそれに当てはめればよいと言う公式も、たくさんあります。

 

たとえば、円錐の側面積の公式。

 

底円の半径をr 、円錐の母線をl とすると、側面の面積は、S = πｒｌ
.

 

底円の半径と、円錐の母線の長さがわかれば、それを入れるだけで側面積が計算できるという、かなり「おとく」な公式です。

 

この公式は『高校への数学・図形のエッセンス』に載っていましたが、塾で中学生を教えるようになって、初めて知りました。

 

高校入試で空間図形がよく出題される高校や、もしかしたら数３の積分計算で、便利に使えるかも知れません。

 

でもこの公式は、果たして覚えておくべきなのでしょうか？ ボクは、覚える必要がない、と思います。

 

こういう公式は、知らないより知っていた方がよいですが、「確か、何か便利な公式があったなあ…」と記憶しているだけでよいのです。

 

「何か便利な公式があったなあ…」と思えば、それは何だったか思い出す事ができます。

 

円錐の側面積を計算するのに、こういう公式があったような記憶があれば、問題を解く時点で、自分で導き出せばよいのです。

 

少ない公式を使いこなすのが大事！

 

たとえばこの場合ですと、なぜそのような公式ができるのか考えればよいので、物理のように文字式で計算していけばいいのです。

 

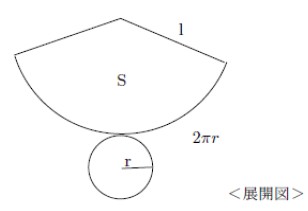
まず底円の半径r から、その円周の長さがわかりますね。

 

2πr です。

 

底円の円周長が、円錐の表面を展開したときのおうぎ形の弧の長さになりますので、この円錐のおうぎ形の面積S は、母線の長さをｌ とすると、となります。

 

この計算が、ふつうの扇形の計算とちょっと違うのは、扇形の面積を計算するために中心角を使っていないところです。

 

扇形が全円だったと考えたときの円周が２πｌ で、その２πｒ分だからこういう計算になります。

 

これを約分すると、S = πｒｌ となるわけです。

 

がこれは数３で習うラジアン（弧度法）の基本的な考え方からすると、当たり前の話ですね。

 

半径が１の円の円周が2π で、それを360°の代わりに使うのがラジアンという角度の単位の「定義」なんですから。

 

つまり公式にはキーになる公式と、そこから導かれる公式・準公式という区別があるわけです。

 

ここでは、円の面積と円周の長さの公式がキーとなる公式で、そこから導かれる円錐の側面積の公式は、覚えなくとも良い公式です。

 

そういうわけで、公式というのは、こういう公式もあったなあ、と覚えておき、必要に応じて作るものなのです。

 

公式は、キーになる公式のみ覚えて、他はそこから導きだしましょう。