問題を解く第2ステップ 既知のモノと、未知のモノ
更新日:

数学問題の解き方。
ポリアの「いかにして問題をとくか」を読む、の続きです。
★既知のモノと、未知のモノとの関連★
いろいろな項目が、おたがいにどんなに関連しているか、また、わからないことが、わかっていることと、どのように結びついているかを知ることが、解がどんなものであるかを知り、計画を建てるために必要である。
「既知のもの」というのは、「問題文の中で与えられた情報」と「問題文には書かれていないが、知っていて当然である知識」のことです。
たとえば問題中に、「△ABC はAB =AC である二等辺三角形である」などと書いてあるのが、問題文中から得られる既知の情報です。
一方「二等辺三角形の底角は等しい、逆に二角が等しい三角形は二等辺三角形である」などという知識( 定理)などは、文外の知識です。
先ほどの例題ですと「円に内接する四角形」が与件なら、「対角の和が180°」というのは知っておかなければならない知識ですね(この問題で使えるかどうかは別の話として)。
そしてもう一方の「未知のもの」というのは、もちろん、問題の答えのことです。
が、その他にも、その問題の背景になっている数学現象なども挙げられます。
入試で出題される問題は、たいてい何かの数学現象から題材を取っています。
フィボナッチ数列は頻出
たとえば東大などでよく出題される「フィボナッチ数列」というのがあります。
フィボナッチ数列というのは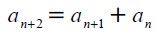
というだけの、簡単な漸化式の数列ですが、偶数項と奇数項で挙動が異なります。
しかも数列の各項は自然数なのに、一般項はなんと複素数で記述されるという、不思議な数列です。
さらに隣り合う項の比を無限大に収束させると、なんと正五角形の対角線などに現れる「黄金比」になってしまうというものです。
ですからこれを使って、さまざまな問題が作れます。
『大数学者に学ぶ数学1 A』( 秋山仁編、数研出版/絶版) には、ウサギの頭数の増え方と、タイルの敷き詰め方、階段の登り方という三種類の問題が載っています。
たしか私が受験した頃の京大の確率の問題などでも、似たような問題があったように記憶しています。
フィボナッチ数列を背景に持つ問題なら、この数列を知っているかどうかが、大きな差になることは容易に理解できるでしょう?












